You can ask questions about our Review for exam 2 here!
Hello, I’m looking at the definitions we need to know for exam 2 and am struggling to find the definitions for “Characteristic polynomial of a matrix A” and “Nonsingular matrix”. where are these in the textbook?
For “Characteristic polynomial of a matrix A”, I used Activity 4.2.2 but could not find a precise definition. for “Nonsingular matrix”, I’m totally lost. Thanks!
2 Likes
Also with the definitions, can we make up our own definitions or do they need to be from the book?
1 Like
I have another question about exam 2. I have no idea how to approach problem 7 on the review sheet (the one about finding the equation of a circle). Do you have any good videos/ readings I could look at that may help with this?
Thanks
1 Like
First off, I’ve updated the review sheet to point to the locations in the text that I’d like you to cite. I’m sorry I didn’t get to that sooner so I’m glad you asked!
I also struck out non-singular so you don’t need to refer to that and replaced it with Invertible in problem #2.
\text{No.}
\text{Yes.}
I presented this in class this past Monday as a fun application of the determinant. You need to know two basic properties of circles together with two basic properties of the determinant to understand this problem:
Circles
- Any three, non-collinear points in the plane determine a unique circle and
- Any circle can be described by an equation of the form
a(x^2+y^2) + bx + cy = d.
Determinants
- The determinant of any matrix with two equal rows is zero and
- Given any three points (x_1,y_1), (x_2,y_2), and (x_3,y_3), the equation\left|\begin{matrix} x^2 + y^2 & x & y & 1 \\ x_1^2 + y_1^2 & x_1 & y_1 & 1 \\ x_2^2 + y_2^2 & x_2 & y_2 & 1 \\ x_3^2 + y_3^2 & x_3 & y_3 & 1 \\ \end{matrix}\right| = 0is the equation of a circle.
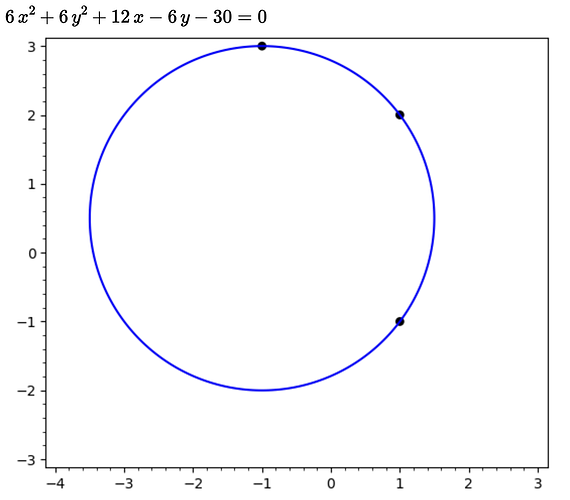
Example
As an example, suppose we’d like an equation of the circle that contains the points (1,2), (-1,3), and (1,-1). Simply use those as your values of (x_1,y_1), (x_2,y_2), and (x_3,y_3) in the determinant based equation above. Thus, you’re equation is
\left|\begin{matrix}
x^2 + y^2 & x & y & 1 \\
1^2 + 2^2 & 1 & 2 & 1 \\
(-1)^2 + 3^2 & -1 & 3 & 1 \\
1^2 + (-1)^2 & 1 & -1 & 1 \\
\end{matrix}\right| = 0.
That’s it! In principle, you could expand that determinant out to illustrate the fact that it has the desired form but there’s no need to.
Illustration
Again, the answer above is fine as is. Here’s a Sage cell to illustrate the process for reinforcement as well. The output looks like so:
