How do I enter groovy, typeset mathematics into a post?

Meta
1

Discourse at Mark’s Math uses LaTeX snippets to input mathematics. Suppose, for example, that I’d like to display this:

If f(x) = e^{-x^2}, then f'(x) = -2x\,e^{-x^2} and

\int_{\infty}^{\infty} f(x) \, dx = \sqrt{\pi}.

I’d enter

If $f(x) = e^{-x^2}$, then $f'(x) = -2x\,e^{-x^2}$ and
$$
\int_{\infty}^{\infty} f(x) \, dx = \sqrt{\pi}.
$$

Here are a few things worth noticing:

  • Typeset math should generally be delimited with dollar signs.
    • Inline math is delimited with single dollar signs $like this$.
    • Display math is delimited with with double dollar signs, each on their own line.
  • Braces are used for grouping {like this}.
  • Exponents are indicated with carets, like this: x^2.
  • Some special operators and functions are prefixed with a backslash, \like_this.
    • \infty is typed like \infty,
    • \pi is typed like \pi,
    • many functions are preceded with a backslash:
      • like \sqrt{x} for \sqrt{x}
      • and \sin(x) for \sin(x),
    • \, will give you a little space.

While it might all seem a bit mysterious at first, it’s not too hard to get the hang of.

Resources

Right here

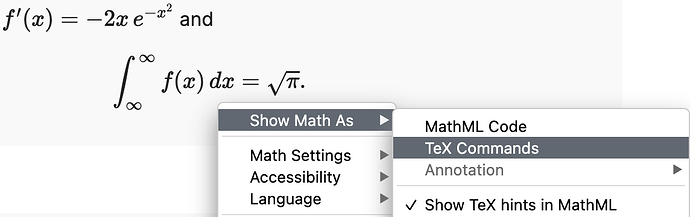
On this forum, you can get the LaTeX code for any typeset mathematics that you see by right clicking or cntrl-clicking on it and selecting
Show Math As :play_button: TeX Commands

That’ll look something like so:

Screenshot 2025-08-07 at 10.08.57 AM
Screenshot 2025-08-07 at 10.08.57 AM1144×360 33.4 KB

AI

These days, of course, you can pose detailed questions to Generative AI for help with all kinds of tasks. Here’s Google’s advice for how to type my favorite integral.

Of course, AI tools are evolving rapidly and I’m not certain what kinds of limits their may be on its use.

More examples

Finally, here’s the code for a few more examples. For each of them, you would need to delimit the code in either single dollar signs for double dollar signs on their own line, depending on whether you want the result inline or in display mode.

Calculus level examples

  • x^2 + \sin(x) yields
x^2 + \sin(x)
  • e^x \cdot \cos(x) yields
e^x \cdot \cos(x)
  • \ln(x^2 + 1) yields
\ln(x^2 + 1)
  • \lim_{x \to 0} \frac{\sin(x)}{x} yields
\lim_{x \to 0} \frac{\sin(x)}{x}
  • \frac{d}{dx} \left( x^3 + 2x \right) yields
\frac{d}{dx} \left( x^3 + 2x \right)
  • \frac{d}{dx} \left( e^x \cdot \cos(x) \right) yields
\frac{d}{dx} \left( e^x \cdot \cos(x) \right)
  • \frac{d}{dx} \left( \ln(x^2 + 1) \right) yields
\frac{d}{dx} \left( \ln(x^2 + 1) \right)
  • \frac{d}{dx} \left( \sin(x^2) \right) yields
\frac{d}{dx} \left( \sin(x^2) \right)
  • \int x^2 \, dx yields
\int x^2 \, dx
  • \int_0^{\pi} \sin(x) \, dx yields
\int_0^{\pi} \sin(x) \, dx
  • \frac{d}{dx} \left( \int_1^x \sqrt{1 + t^4} \, dt \right) yields
\frac{d}{dx} \left( \int_1^x \sqrt{1 + t^4} \, dt \right)
  • \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} yields
\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}

Examples in linear algebra

  • A\vec{v} = \lambda \vec{v} yields
A\vec{v} = \lambda \vec{v}
  • A(\vec{u} + \vec{v}) = A\vec{u} + A\vec{v} yields
A(\vec{u} + \vec{v}) = A\vec{u} + A\vec{v}
  • (AB)\vec{v} = A(B\vec{v}) yields
(AB)\vec{v} = A(B\vec{v})
  • \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{bmatrix}
    \begin{bmatrix} 1 \ 0 \ -1 \end{bmatrix} =
    \begin{bmatrix} -2 \ -2 \end{bmatrix} yields
\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix} = \begin{bmatrix} -2 \\ -2 \end{bmatrix}
  • \begin{bmatrix}
    1 & 0 & 2 & | & 3 \
    0 & 1 & -1 & | & 4 \
    0 & 0 & 0 & | & 0
    \end{bmatrix} yields
\begin{bmatrix} 1 & 0 & 2 & \big| & 3 \\ 0 & 1 & -1 & \big| & 4 \\ 0 & 0 & 0 & \big| & 0 \end{bmatrix}
  • \text{If } A = \begin{bmatrix} a & b \ c & d \end{bmatrix}, \text{ then } \det(A) = ad - bc yields
\text{If } A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \text{ then } \det(A) = ad - bc
  • \vec{v} \cdot \vec{w} = |\vec{v}| |\vec{w}| \cos(\theta) yields
\vec{v} \cdot \vec{w} = \|\vec{v}\| \|\vec{w}\| \cos(\theta)
3 Likes